سوال ۳۱
یک ماتریس $M$ با درایه‌های صفر و یک و با ابعاد $2^n\times 2^n$ موجود است. $S$ رشته‌ی متناظر با ماتریس $M$ را به‌صورت زیر محاسبه می‌کنیم:
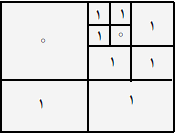
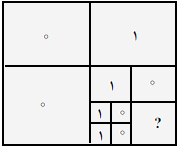
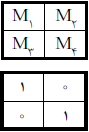اگر کلیه‌ی درایه‌های $M$ صفر باشد، $S=0$ و اگر کلیه‌ی درایه‌های $M$ یک باشد، $S=1$. در غیر این‌صورت ماتریس را به چهار ماتریس مساوی $M_3$، $M_2$، $M_1$ و $M_4$ (مطابق ماتریس بالا از شکل روبه‌رو) تقسیم می‌کنیم. رشته‌ی $S_i$($i=1,2, 3, 4$) متناظر با ماتریس $M_i$ را به‌دست می‌آوریم. سپس $S=2S_1S_2S_3S_4$. برای مثال رشته‌ی متناظر ماتریس پایین از شکل روبه‌رو ۲۱۰۰۱ است.
کدام‌یک از رشته‌های زیر ممکن است رشته‌ی متناظر یک ماتریس صفر و یک باشد؟
\[ \begin{array}{c c c } 1)2022111011111 & 2)2112002000001 & 3)20102102101010 \end{array} \]
- ۱ و ۳
- ۱ و ۲
- ۱ و ۲ و ۳
- ۲ و ۳
- هیچ‌کدام
پاسخ
گزینه (؟) درست است.
ماتریس متناظر به رشته‌ی ۱ ماتریس زیر می‌باشد.
بعد از ٬۲ چهار عدد یکسان نمی‌تواند باشد٬ پس رشته‌ی ۲ ماتریس متناظر ندارد. ماتریس متناظر به رشته‌ی ۳ نیز تا قبل از مرحله‌ی آخر به شکل زیر می‌باشد که در مرحله‌ی آخر ۱۰ را نمی‌توان در خانه‌ی باقی‌مانده قرار داد:
| ▸ سوال قبل | سوال بعد ◂ |