سوال ۱۳
خیکوله مهره‌ی شطرنج جدیدی به اسم «خیل» اختراع کرده است. حرکت این مهره مانند فیل‌های معمولی است با این تفاوت که خانه هایی را روی صفحه‌ی شطرنج تهدید می‌کند که دقیقا دو خانه‌ی قطری (هم از نظر تعداد سطر و هم از نظر تعداد ستون) با آن فاصله داشته باشند. به چند طریق می‌توان در یک صفحه‌ی شطرنج $۸\times ۸$ دو مهره‌ی خیل متمایز قرار داد که‌یکدیگر را تهدید نکنند؟
- ۱۸۷۲
- ۳۸۸۸
- ۱۱۴۴
- ۱۹۴۰
- ۲۲۸۸
راهنمایی
سعی کنید حالات نامطلوب قرارگیری دو مهره را بشمارید.
راهنمایی
اگر دو مهره‌ی خیک یکدیگر را تهدید کنند، بر دو گوشه‌ی یک مربع $3 \times 3$ قرار دارند.
راهنمایی
تعداد مربع‌های $3 \times 3$ ضربدر در تعداد حالات قرارگیری مهره‌ها داخل آن‌ها را می‌بایست از کل حالات کم کرد.
پاسخ
گزینه‌ی ۲ درست است.
حالات غیرمعتبر را از کل حالات قرارگیری دو خیل در صفحه‌ی شطرنج کم می‌کنیم.
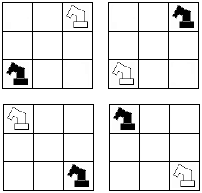
وقتی دو خیل همدیگر را تهدید می‌کنند که در دو قطر یک مربع $3×3$ باشند. چون رنگ خیل‌ها باهم فرق دارد به چهار حالت زیر می‌توانند در قطر قرار بگیرند.
همچنین به ۳۶ حالت می‌توان جدول $3×3$ را در جدول اولیه مشخص کرد. درنتیجه جواب نهایی برابر است با:
$$64×63-4×36=3888$$
| ▸ سوال قبل | سوال بعد ◂ |